1 原子核是相對論體系還是非相對論體系?
原子核是由質子和中子組成的量子多體系統。無論從1911年盧瑟福提出原子有核,還是從更早一些放射性的發現算起,原子核物理研究都已走過了百年的歷程。但是,關于原子核是相對論還是非相對論體系,至今還有爭議。
諾貝爾獎獲得者玻爾和莫特爾松在其經典教科書中指出,根據費米氣體模型,核子的動能大約為40 MeV,遠小于其約1000 MeV的質量,相對論效應很小,因此可以將原子核看作非相對論體系。根據實驗觀測,從原子核中移走核子需要的能量大約為10 MeV,從而估計出原子核的平均勢大約為-50 MeV,以此平均勢為基礎建立的原子核殼模型自然是非相對論的模型,原子核當然也被視為非相對論體系。
這個原子核被視為非相對論體系的結論,是在假設原子核體系服從非相對論量子力學的基礎上提出的。而且,在非相對論理論中,為了正確描述特別穩定的原子核對應的核子數,即幻數,需要唯象地引入自旋軌道相互作用。而相對論理論則可以自然地給出自旋軌道相互作用。
隨著核物理研究的深入,越來越多的證據更傾向于將原子核視為相對論體系:
(1)核子結合成原子核會放出能量,即質量虧損,而質量虧損就是一個相對論效應;
(2)相對論協變性的要求可以減少模型參數,使模型有更好的預言能力,滿足強相互作用的基本理論,即量子色動力學的精神;
(3)在非相對論理論中,核子在約為-50 MeV的平均勢場中運動。而在相對論理論中,核子滿足的運動方程中的標量勢和矢量勢約為500 MeV量級,其相對論效應不可忽略;
(4)相對論理論自然給出自旋軌道相互作用。非相對論理論需要唯象地引入自旋軌道相互作用;
(5)長期存在的贗自旋對稱性起源之謎,以及與之相應的反核子譜的自旋對稱性,只能在相對論理論框架下得以解釋;
(6)對于時間反演對稱性破缺的體系,奇時間勢場在相對論框架下由矢量勢的空間分量自然給出,而在非相對論框架下則需要引入額外的參數;
(7)在對無限大核物質的第一性原理研究中,相對論Brueckner—Hartree—Fock(RBHF)方法可以較好地給出飽和點性質,而非相對論理論需要唯象地引入三體相互作用才能給出合理的描述;
(8)相對論密度泛函理論在實際應用中有更好的普適性,適用于描述更大范圍的原子核性質。
基于以上原因,我們有足夠的理由發展相對論理論來研究原子核性質。
2 原子核結構的相對論密度泛函
如何從強相互作用理論出發,對原子核的單核子運動和集體運動進行微觀和自洽的統一描述,是核物理學家需要解決的問題。特別是,如何基于核子—核子相互作用,研究原子核的結構和反應,復雜原子核結構中出現的規律和簡單模式,以及原子核性質隨質量、同位旋、角動量和溫度等的演化。
密度泛函理論最初在研究庫侖系統時被提出,如今廣泛應用于處理復雜的量子多體問題。它的基礎是霍恩伯格—科恩(Hohenberg—Kohn)定理。該定理指出,一個外場中的多粒子體系的基態能量,可以寫為該體系密度的一個普適的泛函。密度泛函理論的實用性,取決于所構建的密度泛函是否準確。Kohn和Sham提供了構建能量密度泛函的一個實用方法。該方法將有相互作用的多體系統,映射到虛構的無相互作用系統,并假設該無相互作用系統的基態密度等于真實的基態密度,如圖1所示。對該無相互作用系統應用Hohenberg—Kohn定理,可以導出一個自洽求解的單粒子運動方程。形式上,Kohn—Sham密度泛函理論的求解,與Hartree—Fock方法類似。但是,它僅包括定域項,避免了處理復雜的非定域項。Hartree—Fock理論中復雜的積分微分方程,被簡化為簡單的微分方程,即Kohn—Sham方程。密度泛函理論廣泛地應用于化學、材料科學、凝聚態物理等領域。
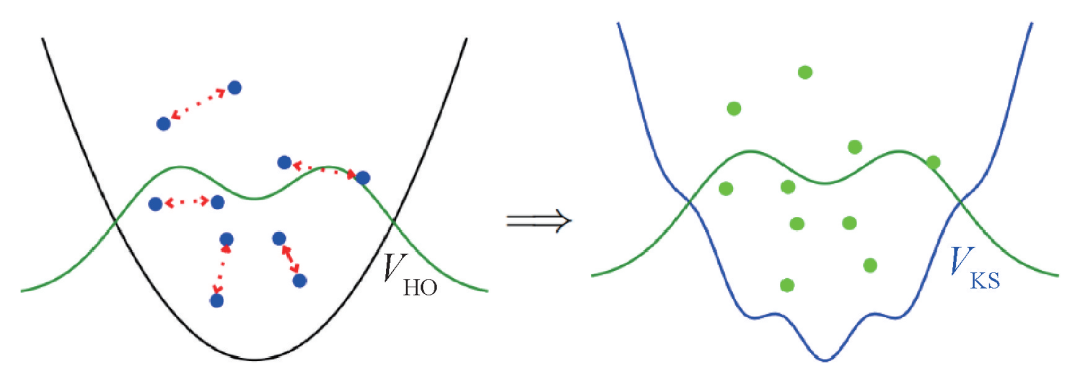
圖1 Kohn—Sham 密度泛函理論示意圖。左圖展示諧振子勢場中的相互作用系統,右圖展示 Kohn—Sham 勢場中的無相互作用系統。兩個系統的基態密度相同,由綠色實線表示
在原子核物理中,密度泛函理論適用于描述核素圖中幾乎所有原子核的基態性質,是研究穩定原子核和遠離穩定谷的奇特原子核的重要工具。
庫侖系統中,能量的密度泛函可以從庫侖相互作用導出。原子核物理中的密度泛函理論是有效理論,原子核的基態能量是各種密度和流、以及它們的梯度的泛函,通過擬合有限核的實驗數據確定其中的參數。傳統上,密度泛函理論在核物理中的應用,大多采用非相對論的形式。
與傳統的非相對論原子核理論相比,相對論密度泛函理論從拉格朗日量出發,考慮了洛倫茲不變性,為構建有效核子—核子相互作用提供了更根本、更微觀的方案。
在基于介子交換圖像的相對論密度泛函理論中,核子為狄拉克粒子,核子之間通過交換介子發生相互作用。交換的介子包括標量—同位旋標量、矢量—同位旋標量、標量—同位旋矢量和矢量—同位旋矢量等介子。為了對核物質和原子核表面性質進行合理描述,需要考慮核子—介子頂角的密度依賴性,即需要在拉格朗日量中引入非線性的介子自相互作用或者耦合參數的顯式密度依賴。具體計算中,需要求解核子滿足的狄拉克方程和介子滿足的克萊因—戈爾登方程。由于涉及耦合的非線性微分積分方程組,求解頗為復雜。
利用核子之間的定域相互作用代替各個耦合道的介子交換,引入高階耦合或者耦合參數的密度依賴性考慮介質效應,可導出基于點耦合相互作用的相對論密度泛函理論。由于避免了介子自由度,降低了求解的復雜性,易于推廣進行超越平均場的計算,點耦合相對論密度泛函理論近年來得到了較快的發展。
基于介子交換和點耦合相互作用的相對論密度泛函理論,已成功地描述從有限原子核到無限大核物質,從穩定原子核到遠離穩定谷的奇特原子核,從球形原子核到任意形狀的原子核,從基態到激發態,從通常的核物質到具有奇異自由度的超核物質的性質。相對論密度泛函理論還被廣泛用于研究致密星體的狀態方程,以及天體環境下的核合成過程涉及到的重要核物理量。
現有的相對論密度泛函理論中,北京大學研究團隊基于點耦合相互作用提出的PC-PK1(PC是點耦合point-coupling的縮寫,PK指北京大學,1是序號),給出了原子核質量最高精度的密度泛函描述,對原子核的基態性質描述取得了很大的成功。對于已有實驗數據的575個偶偶原子核,PC-PK1的描述精度達1.14 MeV。PC-PK1的成功之處在于,它正確地考慮了原子核性質的同位旋依賴性,很好地描述了球形原子核的質量。對于形變原子核,考慮動力學關聯,可以進一步改善對原子核質量的描述。與之相比,一些密度泛函理論,由于沒有正確描述原子核質量的同位旋依賴性,即使考慮動力學關聯,也不能改善對原子核質量的整體描述。
除了描述基態性質,PC-PK1密度泛函理論還被推廣用于描述原子核的激發態性質,例如磁轉動、反磁轉動、形狀相變和手征轉動等[2]。最近,有文獻基于PC-PK1,在三維空間格點上,發展了不限制任何對稱性的含時相對論密度泛函理論,為研究原子核的動力學性質提供了新的途徑。
3 原子核基態
自然界中穩定的原子核有244種,壽命大于十億年的原子核有41種。通過對這些原子核的研究,建立了獨立粒子殼模型和集體運動模型等原子核模型,構建了相應的核物理知識體系。自20世紀末起,隨著稀有同位素大科學裝置和相關探測設備的建造和運行,合成了大量遠離穩定谷的原子核,也被稱為奇特原子核。在這些原子核中,發現了許多與傳統核物理知識相悖的新現象。例如,暈現象,即奇特原子核中出現的半徑異常增大的現象,對傳統知識中的核物質不可壓縮性提出了挑戰;幻數的改變,即奇特原子核中傳統幻數的消失和新幻數的出現,對傳統的獨立粒子殼模型提出了挑戰。奇特原子核中的費米面接近連續譜閾值,部分核子處于弱束縛狀態,對關聯效應增強,能夠將配對的核子散射到連續譜中。因此,研究奇特原子核性質必須考慮連續譜和核子配對等效應。
基于相對論密度泛函,利用博戈留波夫(Bogoliubov)準粒子變換考慮對關聯,在坐標空間自洽求解準粒子運動方程,正確考慮連續譜效應,由此發展的相對論連續譜Hartree—Bogoliubov(RCHB)理論,微觀自洽地描述了實驗上發現的第一例暈現象,揭示了連續譜對暈核的貢獻,在研究中等質量和重質量的奇特原子核時,預言了由多個暈核子組成的巨暈現象。基于RCHB理論,利用PC-PK1密度泛函,建立了迄今唯一考慮連續譜效應的RCHB原子核質量表。
除了質子數和中子數都是幻數的原子核,核素圖中的大多數原子核,形狀都偏離球形。因此,研究遠離穩定谷的奇特原子核,除了上面提到的連續譜和對關聯效應,還必須考慮形變自由度的影響。通過在坐標空間求解伍茲—薩克森(Woods—Saxon)勢的狄拉克方程,得到包含費米海和狄拉克海的單粒子空間,構建完備的狄拉克Woods—Saxon基。利用正確考慮連續譜漸近行為的狄拉克Woods—Saxon基,對原子核的密度和勢場進行勒讓德展開,正確考慮軸對稱形變、對關聯和連續譜效應,發展了微觀自洽的形變相對論連續譜Hartree—Bogoliubov(DRHBc)理論。基于DRHBc理論,不僅預言了42, 44Mg是形變暈核,而且揭示了形變暈核中可能存在的形狀退耦現象,即核芯和暈核子部分具有不同的四極形變,被認為是滴線附近原子核有趣的新現象之一。
DRHBc理論在RCHB理論的基礎上考慮了形變效應,結合目前對原子核質量描述最為成功的相對論密度泛函PC-PK1,有望構建包含連續譜和形變效應并且有預言能力的微觀高精度原子核質量表。為此,由北京大學發起,聯合韓國基礎科學研究所、中國科學院理論物理研究所和香港大學等16個研究所和高校,成立了DRHBc質量表合作組。
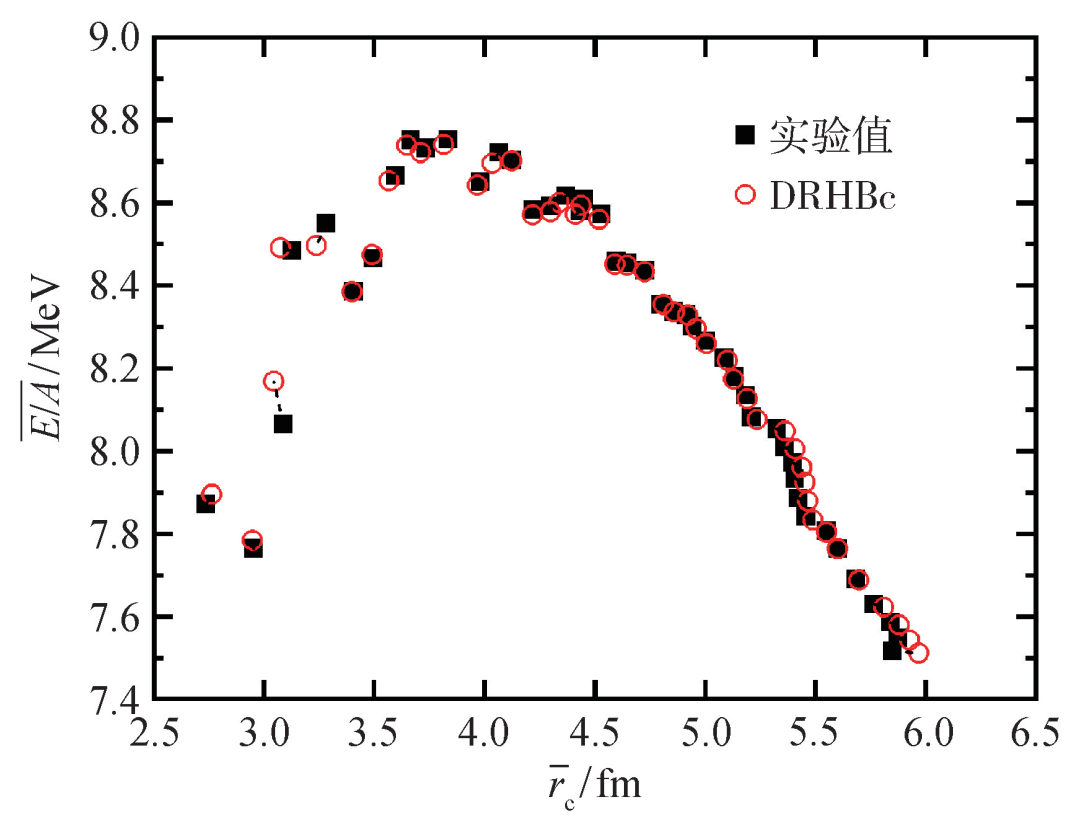
圖2 根據文獻給出的計算方案,DRHBc理論計算的從氧到鋦的每一個同位素鏈,偶偶原子核的平均比結合能和平均電荷半徑。實心方塊表示實驗值,圓圈表示DRHBc理論的計算結果,點線連接著同一個同位素鏈的實驗和理論值
目前,DRHBc質量表合作組已完成偶偶核的計算。在質子數8≤Z≤120范圍內,給出了2583個束縛偶偶原子核的質量。對于已有實驗數據的638個偶偶核,DRHBc理論的描述精度為1.52 MeV,是目前微觀理論給出的最高精度之一。對于由上百個質量約為1000 MeV的核子組成的原子核,精度已經高達10-5。如果考慮原子核的三軸形變自由度,利用更微觀的方法考慮動力學關聯能,有望進一步提高精度。對于已有電荷半徑實驗數據的369個偶偶原子核,DRHBc理論的描述精度達0.03 fm(1 fm=10-15 m),均方根偏差為0.70%。為了展示理論計算與實驗值的整體符合程度,圖2給出了從氧到鋦每一個同位素鏈,偶偶原子核的平均比結合能 和相應的平均電荷半徑
和相應的平均電荷半徑 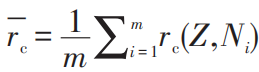 。
。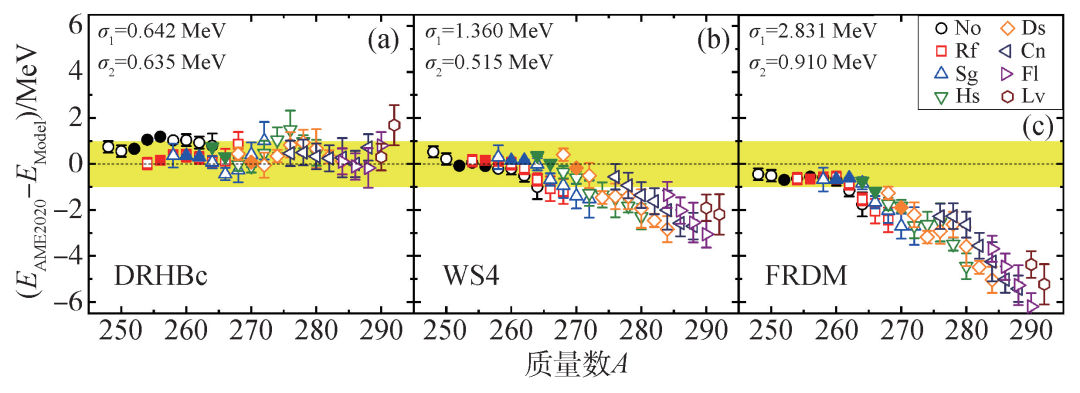
圖3 超重偶偶原子核的最新質量評估數據 AME2020,對 DRHBc 理論(a),和高精度宏觀微觀質量模型 WS4(b)以及 FRDM(c)預言能力的檢驗。AME2020 給出的 10 個質量實驗數據用實心符號表示,46個質量經驗值用空心符號表示。σ1表示對全部數據的描述精度,σ2表示對10個實驗數據的描述精度
為了進一步檢驗DRHBc理論的預言能力,圖3(a)給出了超重偶偶原子核計算結果與最新質量評估數據AME2020的偏差。作為對比,圖3(b),(c)給出了高精度的宏觀微觀質量模型WS4和FRDM的相應結果。DRHBc理論對實驗值的預言精度為0.635 MeV,相應的WS4和FRDM精度分別為0.515 MeV和0.910 MeV。對全部實驗和經驗數據,DRHBc理論的預言精度為0.642MeV,相應的WS4和FRDM精度分別為1.360 MeV和2.831 MeV。由于DRHBc理論正確地描述了原子核質量的同位旋依賴性,因此預言能力有更高的可靠性。
4 原子核的手征轉動
手征對稱性在自然界中廣泛存在,如人的左右手、海螺殼的螺旋性、化學分子的手性等。幾何學中,如果一個圖像與其鏡像不同,或者不能通過轉動或平移操作,使其與鏡像重合,則稱該圖像是手性的,或者說具有手征性。化學中,手性分子的研究和應用是一個非常活躍的領域,涉及有機化學、生物化學和超分子化學等領域,2001年和2021年的諾貝爾化學獎就與手性分子合成有關。粒子物理學中,手征對稱性是區分無質量粒子的內稟自旋平行或者反平行于其動量的動力學性質。
1997年,Frauendorf和孟杰預言了原子核中的手征對稱性[18]。他們指出,一個具有特殊三軸形變的原子核,處于高角動量軌道上的核子粒子和空穴,相應的角動量方向將分別沿原子核質量分布的短軸和長軸,其余核子組成的原子核核芯,最大的轉動慣量方向對應中間軸。這樣的體系,粒子、空穴和核芯的角動量相互垂直,與總角動量一道,在本體系中形成能量完全簡并的左手和右手體系。在實驗室坐標系中,由于手征對稱性破缺,在一定的角動量范圍內,將出現兩條能量近簡并的轉動帶,即原子核中手征對稱性的實驗信號。
2001年,美國紐約大學石溪分校的科學家,利用耶魯大學的實驗設施,在中子數為75的130Cs,132La,134Pr和136Pm 4個原子核中,觀測到理論預言的手征雙重帶,證實了手征對稱性的存在。迄今為止,實驗上已經在質量數為80、100、130和190的核區,發現了50余例手性原子核,即存在手征雙重帶的原子核。目前,研究手性原子核的理論模型包括粒子轉子模型、傾斜軸推轉方法、無規相位近似方法、集體哈密頓量方法和投影殼模型等。
2006年,意大利等國的科學家測量了134Pr的電磁躍遷幾率,結果發現與理論預期不符,為手性原子核的研究蒙上了陰影。為了解決該問題,同時針對當時的手性原子核理論多基于唯象模型,亟需發展微觀理論預言手性原子核,以配合實驗探索。北京大學研究團隊發展相對論密度泛函理論,微觀描述原子核形變以及高角動量軌道的核子粒子和空穴,正確預言手性原子核。他們發現,一個原子核中可能存在基于不同三軸形變或者核子粒子空穴激發的多對手征雙重帶現象,并把這一現象命名為多重手征雙帶,簡稱MχD。MχD的預言激發了美國阿貢國家實驗室等多個實驗室進行相關實驗。2013年,在實驗和理論同行的共同努力下,在133Ce中發現兩對手征雙重帶,證實了MχD的理論預言。
最近,無需假設任何對稱性,在三維格點空間發展的含時相對論密度泛函理論已被成功用于研究手征原子核的動力學性質[22]。無需引入參數,理論計算結果不僅很好地再現了135Nd中觀測到的兩對手征雙重帶的能譜,而且揭示了原子核手征轉動的動力學新機制,即圖4所示的手征進動。
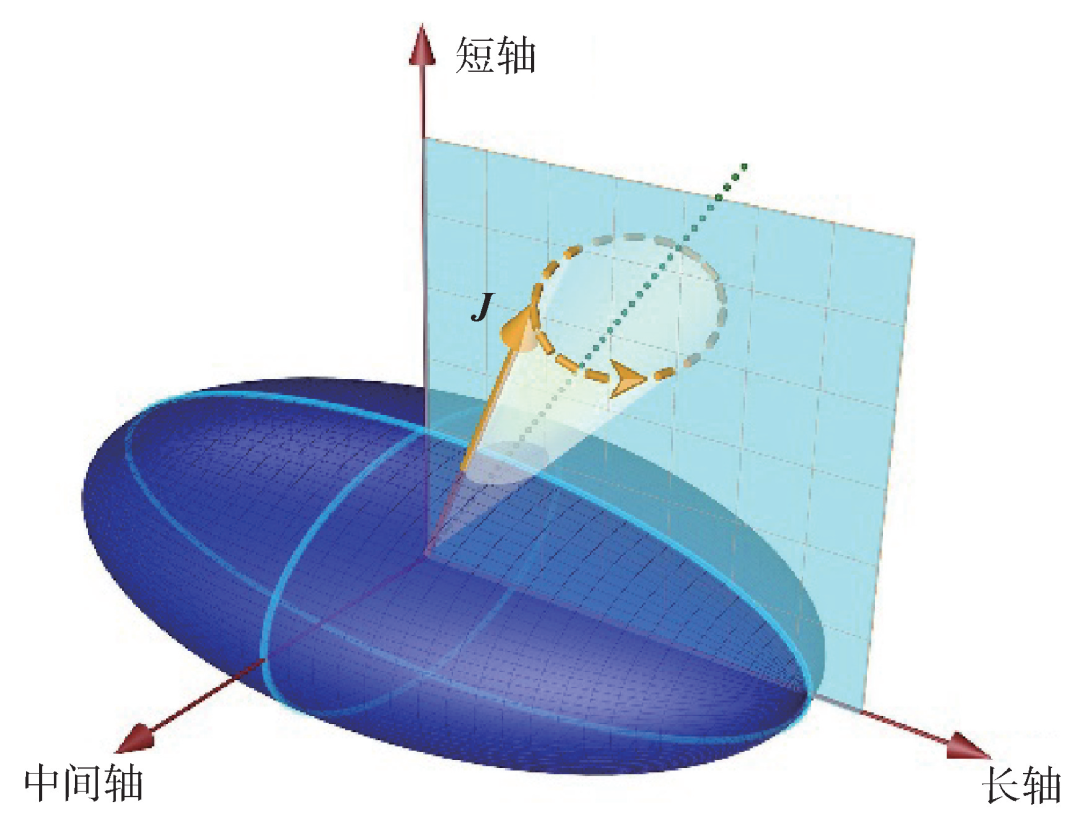
圖4 手性原子核的手征進動示意圖。原子核的總角動量J繞著本體系中點虛線所示的軸轉動
以135Nd為例,推轉相對論密度泛函理論計算,在給定角動量時,給出(θJ,φJ )平面上的能量曲面,如圖5(a)所示角動量為I = 31/2 ?時的能量曲面。其中,θJ 是原子核總角動量和長軸的夾角,即極角,φJ 是總角動量在中—短平面上的投影和短軸的夾角,即方位角。圖中,兩個極小點的能量簡并,θJ 相同,φJ 符號相反,分別對應著角動量I = 31/2 ?時的左手態和右手態。由于推轉相對論密度泛函理論計算是在固定于原子核上的坐標系中進行的,因此只能給出一對能量簡并的手征雙重帶。
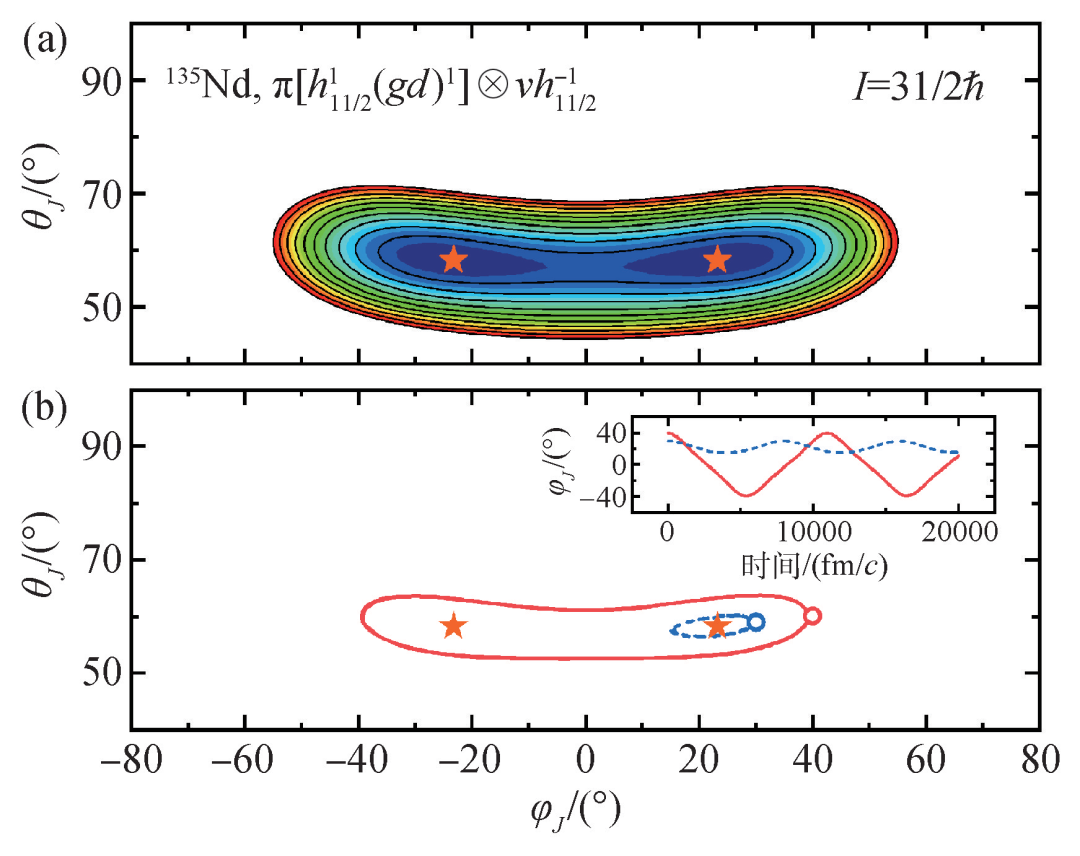
圖5 (a)135Nd 在角動量 I=31/2 ? 時,推轉相對論密度泛函理論計算給出,在角動量取向角(θJ,φJ )平面的能量曲面,對應的粒子空穴組態為 π[h111/2 (gd )1]⊗νh111/2,五角星表示能量極小值;(b)從圓圈表示的兩個不同的初始態出發,含時相對論密度泛函理論在(θJ,φJ )平面上給出的演化路徑分別用實線和虛線表示。插圖展示方位角φJ隨時間的演化
為了微觀自洽地給出135Nd中觀測到的手征雙重帶的能級差,需要考慮超越平均場近似的關聯效應。對于給定角動量,從推轉相對論密度泛函理論給出的能量曲面上的任意一點出發,在實驗室坐標系下進行含時演化,即可得到總角動量的極角θJ 和方位角φJ 隨時間的演化。演化路徑在(θJ,φJ)平面上形成閉合的曲線。圖5(b)給出從兩個不同的初始態出發,總角動量在(θJ,φJ)平面的演化路徑,分別用實線和虛線表示。如果初始態的能量低于兩個極小值之間的位壘,如圖中虛線所示,演化路徑為橢圓,以相應的極小值為中心,即總角動量圍繞能量極小所對應的軸轉動。根據方位角φJ隨時間的演化,利用傅里葉變換,可提取手征激發能,給出手征雙重帶的能級差,從而微觀自洽地描述實驗上觀測到的手征雙重帶和原子核手征轉動的動力學機制,即手征進動。如果初始能量高于兩個極小值之間的位壘,如圖5(b)中實線所示,演化路徑會經過兩個極小值對應的區域,這涉及左手態與右手態之間的量子隧穿,需要更復雜的重新量子化或生成坐標方法進行處理。
5 原子核的動力學性質
原子核的動力學過程,如散射、裂變和聚變等,同樣可以基于相對論密度泛函理論進行研究。
Hoyle態,即12C的第二個0+態,對于宇宙核合成和生命起源至關重要。在Hoyle態中,三個4He的結團是否為鏈式結構,一直是實驗和理論研究的熱點。推轉相對論密度泛函理論研究表明,讓原子核轉動或者增加中子數目都有助于增強鏈式結構的穩定性。利用含時相對論密度泛函理論,研究4He+8Be和4He+10Be的共振散射,通過考察密度分布及其隨時間的演化,揭示了鏈式結構的動力學特征。

圖6 初始質心能量為 2 MeV 的正面碰撞過程中,含時相對論密度泛函理論在t =100,1200,3300,5000 fm/c 時刻,給出的 4He+8Be(左)和 4He+10Be(右)在 xz 平面的密度分布
對于初始質心能量為2 MeV的正面碰撞,圖6展示了含時相對論密度泛函理論給出的4He+8Be和4He+10Be在xz平面的密度分布隨時間的演化。兩個碰撞體系隨著時間演化,均出現鏈式結構。對于4He+8Be,鏈式結構持續至3100 fm/c(1 fm=10-15 m,c是光速),隨后開始彎曲,形成如圖6(c)所示的類三角結構,最后演化成如圖6(d)所示的近球形形狀。演化過程中出現的彎曲,破壞了體系的軸對稱性,導致了鏈式結構的不穩定,表明不假設任何對稱性,微觀地研究原子核鏈式結構動力學性質的重要性。對于4He+10Be,鏈式結構可以持續至5000 fm/c以上。隨著時間演化,4He結團和10Be結團的位置會發生交換,出現準周期振蕩,如圖6(f),(g)所示。與4He+8Be相比,增加的兩個中子減慢了結團結構的準周期振蕩,即動力學同位旋效應,導致4He+10Be碰撞產生的鏈式結構更加穩定。
6 原子核結構的相對論第一性原理研究
相對論密度泛函理論基于一個普適的拉氏量密度,可以對核素圖中幾乎所有原子核的基態和激發態性質進行描述。然而,相對論密度泛函中涉及到的十余個參數不能從第一性原理導出,而是通過擬合原子核的實驗數據確定。在這個意義上,相對論密度泛函理論是一個有效理論。特別是,在原子核結構研究中有重要影響的張量力,其效應與自旋軌道勢的效應耦合在一起,難以通過實驗數據唯一確定。此外,利用第一性原理計算,研究特殊的物理觀測量,可以為相對論密度泛函的構建提供重要參考。
由于過高的計算機資源需求,過去數十年中,一直沒有實現原子核真正意義上的相對論第一性原理計算。通常的做法是,首先通過自洽的核物質相對論Brueckner—Hartree—Fock(RBHF)計算,提取有效相互作用的密度依賴性,然后將其映射到有限原子核,進行有限原子核的相對論Hartree—Fock計算,即有效密度近似(EDA)。然而,這種映射并不唯一,有很大的不確定性。
原子核結構的相對論第一性原理計算最近取得了突破。從相對論形式的真實核子—核子相互作用Bonn勢出發,利用完全自洽的狄拉克Woods—Saxon基求解了有限原子核的RBHF方程,不引入任何自由參數,實現了原子核基態性質的相對論第一性原理計算。
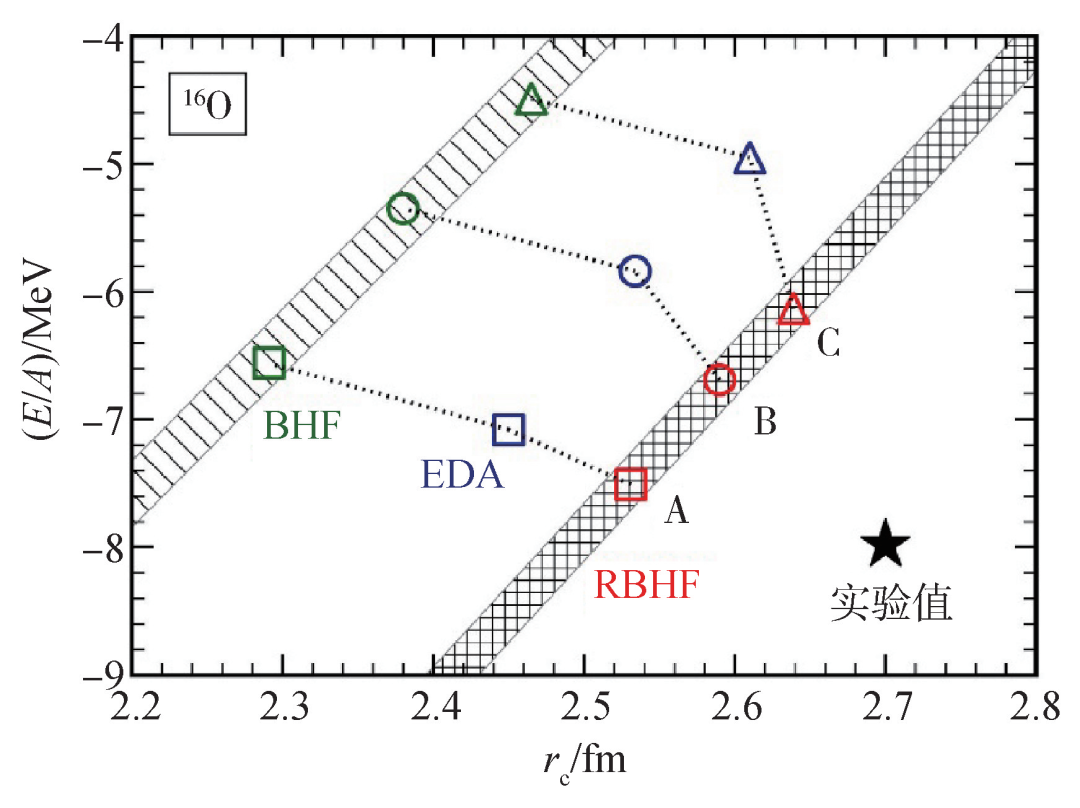
圖7 利用 Bonn A 和 B 以及 C 三種核子—核子相互作用, 以 16O 為例,相對論第一性原理 RBHF 計算給出的比結合能和電荷半徑,與實驗值、非相對論 BHF 計算和采用 EDA 近似的結果比較。線性條帶突出顯示 RBHF 和 BHF 的計算結果
以16O為例,利用德國Bonn大學發展的三種核子—核子相互作用Bonn A,Bonn B,Bonn C,圖7展示了完全自洽的RBHF理論計算給出的比結合能和電荷半徑,以及與實驗值、非相對論BHF計算結果和采用EDA近似的比較。結果表明,相對論第一性原理計算,顯著改善了對結合能和電荷半徑的描述。RBHF計算結果顯著優于EDA近似,這表明自洽性十分重要。
關于RBHF理論的成功和影響,可參見綜述文獻。它回顧了基于唯象平均場、有效核子—核子相互作用和真實核子—核子相互作用建立模型,研究原子核結構的歷史。綜述了完全自洽的RBHF理論對有限核和中子滴系統的研究現狀。提出了基于真實核子—核子相互作用,進行核物質和有限原子核的第一性原理計算,建立相對論第一性原理密度泛函的基本思想。
7 總結和展望
經過幾十年的努力,基于密度泛函理論和量子場論建立起來的相對論密度泛函理論,得到很大發展,解決了非相對論理論中難以解釋的贗自旋對稱性起源之謎,自洽包含了非相對論理論中需要唯象引入的自旋軌道勢和奇時間場,成功地描述了各種原子核現象。基于真實核力的相對論第一性原理計算,自然給出核物質飽和點性質,無需像非相對論計算那樣唯象引入三體相互作用。近來,不假設任何對稱性,在三維坐標格點空間發展的含時相對論密度泛函理論,微觀地揭示了原子核手征轉動的動力學新機制和原子核鏈式結構的動力學特征,有望在原子核的聚變和裂變反應以及超重原子核合成等方面發揮重要作用。
原子核物理的相對論第一性原理研究,即完全自洽的相對論Brueckner—Hartree—Fock理論,在描述無限大核物質和有限原子核等方面取得了很大成功,表明了相對論第一性原理計算的可行性和優越性。基于相對論第一性原理研究,可以為構建普適的相對論密度泛函提供重要參考。例如,通過相對論第一性原理研究原子核系統,提取難以通過實驗數據確定的張量力效應等。此外,對實驗無法提供的高密度核物質性質等,相對論第一性原理研究可以提供重要參考和約束,指導構建基于第一性原理的普適的相對論密度泛函理論,實現對原子核的結構和反應性質以及中子星等致密天體狀態方程的完全微觀自洽描述。