攪拌摩擦焊(FSW)是一種適用于鋁合金等低熔點合金板材焊接的新型固態焊接技術,與傳統熔焊焊接工藝相比具有焊接質量易控、焊接精度高等優點,已經成為近年來鋁合金焊接工藝的發展趨勢。
焊接接頭的疲勞壽命估算是軌道交通車輛疲勞評估的核心內容,也一直是車輛設計與制造過程中的難點。目前一般方法是根據疲勞評估標準,通過有限元仿真計算分析焊縫附近的應力,同時通過動力學仿真或動應力試驗獲得焊縫區域的載荷譜,基于應力計算結果和載荷譜計算焊縫的疲勞壽命。這類評估結果的準確性與模型精度直接相關,結合疲勞試驗驗證可獲得更加可靠的評價結果,但試驗成本高、時間長,應用條件受限,基于有限元仿真的疲勞壽命估算結果往往得不到有效驗證。
相關研究表明,疲勞損傷引起的非線性效應會導致超聲檢測信號中出現特殊頻率的信號成分,利用非線性超聲檢測手段可對疲勞損傷進行檢測,獲取與疲勞壽命相關的檢測信號特征,實現疲勞壽命的無損評價。
在疲勞損傷的非線性超聲檢測領域,國內外學者已取得了多種研究成果。基于這些研究成果,筆者以FSW接頭為研究對象,提出了一種基于超聲檢測的焊縫疲勞壽命估算方法。該方法采用非線性超聲檢測手段評價焊縫中疲勞損傷的累積程度,根據疲勞壽命與超聲檢測信號特征的相關關系來評價焊縫的疲勞壽命,具有成本低、可靠性高等優點,可望推動疲勞壽命評價方法的技術發展。
01
疲勞損傷的非線性超聲檢測原理
超聲波在固體介質中的傳播可由函數u(x,t)表示,該函數表示傳播時間為t、傳播距離為x處的聲波振動幅度,遵循如下波動方程:
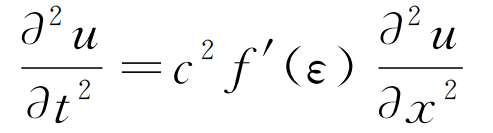
(1)
式中:c為超聲波的傳播速度;f(ε)為關于應變ε的函數,由應力σ與應變ε的關系決定,即:
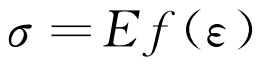
(2)
式中:E為介質的彈性模量。
對于線性介質,有f(ε)=ε。受組織不均勻及材料內部微小缺陷影響,超聲波的傳播介質會表現出非線性效應,即f(ε)中還會出現ε的二次項及高次項,此時f(ε)可根據泰勒公式近似分解為:
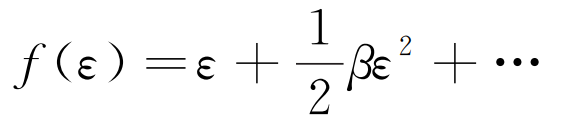
(3)
式中:β為二次非線性系數,以下簡稱非線性系數。
超聲波一般由單一頻率的正弦波激勵,在起始位置有如下形式:
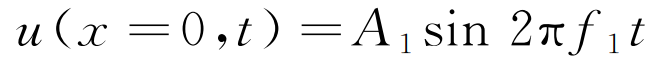
(4)
式中:A1為超聲波基波的幅值;f1為超聲波的頻率。
將式(3)代入式(1),并將式(4)作為邊界條件,可求解得到:
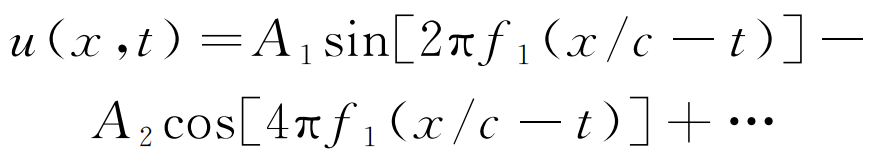
(5)
式中:A2為二次諧波的幅值,可表示為:
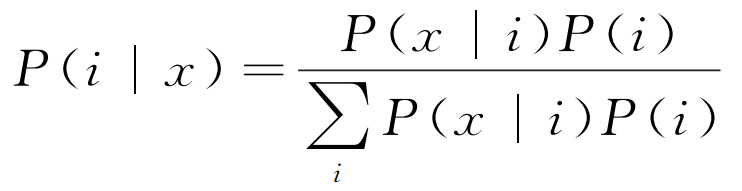
(6)
式(5)中右側第一項表示基波成分,第二項表示二次諧波成分(其信號頻率是基波頻率的兩倍),其余項為三次及更高階次的諧波成分;由于高次諧波的能量占比非常小,非線性超聲檢測中一般只考慮二次諧波成分。
對于同組超聲檢測中由不同試件得到的同一處回波信號而言,其傳播距離x、基波頻率f1及波速c一般不會改變,則有:
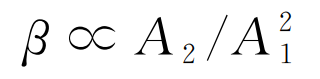
(7)
根據式(7),可通過測量基波和二次諧波的幅值,分析β的相對大小。
與基于基波的傳統超聲檢測相比,非線性超聲檢測中的諧波信號對材料中包括疲勞損傷在內的微小損傷更為敏感。材料疲勞過程中會產生微小的疲勞損傷并逐漸累積,由這些疲勞損傷引起的非線性效應也會逐漸增強。因為β可表征非線性效應的大小,所以根據β的變化趨勢可分析疲勞損傷的發展過程,進而實現材料疲勞壽命的無損評價。
02
非線性超聲檢測方案
檢測對象
選取厚度為8 mm,材料為6005A-T6的鋁合金擠壓板材進行了單軸肩FSW對焊,焊后將焊接接頭磨平,按照圖1所示尺寸進行取樣加工,制備得到FSW焊接試件。
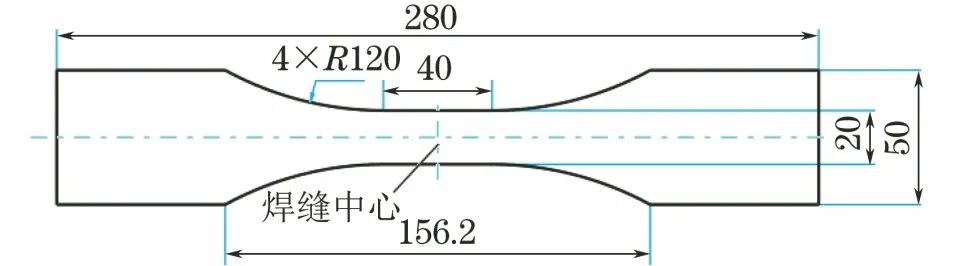
圖1 FSW焊接試件尺寸示意
參照標準GB/T 3075-2008《金屬材料 疲勞試驗 軸向力控制方法》對焊接試件進行階段性疲勞試驗,采用正弦變化的交變載荷進行加載,加載頻率約為100 Hz,應力比為0.1,設置最大應力為120 MPa。取預期疲勞壽命為N0(107次),將試件分別疲勞至0.1N0,0.3N0,0.5N0,0.7N0,且不出現疲勞失效,即可獲得10%,30%,50%,70%壽命的階段性疲勞試件。每個階段各獲取8個試件,另取8個未疲勞試件記為0%壽命階段作為對比。對各階段試件(共40個)進行非線性超聲檢測,可分析得到檢測信號特征與疲勞壽命的相關關系,并據此研究焊縫疲勞壽命的評價方法。
檢測系統
采用RITEC公司的RAM-5000 SNAP型非線性超聲檢測系統發射和接收超聲波信號,同時配合帶通濾波器、前置放大器等信號處理模塊,提取檢測信號的基波及二次諧波成分,非線性超聲檢測系統結構框圖如圖2所示。
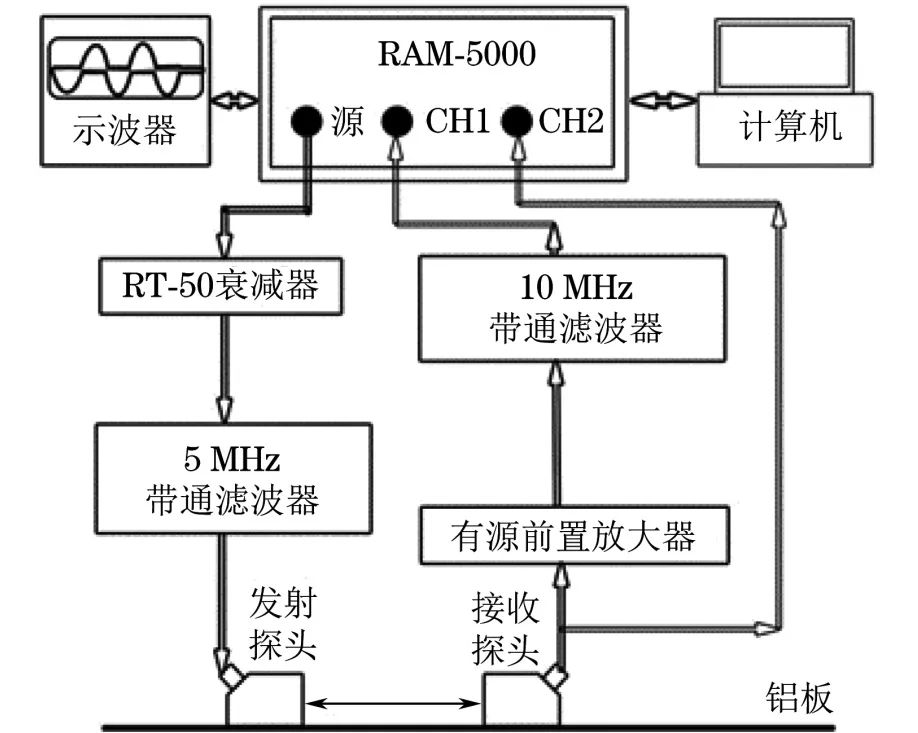
圖2 非線性超聲檢測系統結構框圖
系統工作時,激勵信號經5 MHz帶通濾波器處理后,由發射探頭傳播進入試件中;采用寬帶探頭接收信號,其中基波信號直接傳入信號接收器,同時通過10 MHz帶通濾波器提取二次諧波信號并傳入另一路信號接收器。
采用如圖3所示的接觸式雙斜探頭檢測方式對階段性疲勞試件進行檢測。定制斜探頭的發射角度,使超聲波在試件中形成折射角為45°的橫波;調整探頭位置使兩個探頭對應的折射點距離為32 mm(試件厚度的4倍),由此可以接收到超聲波在試件內經兩次底面反射后的回波信號。
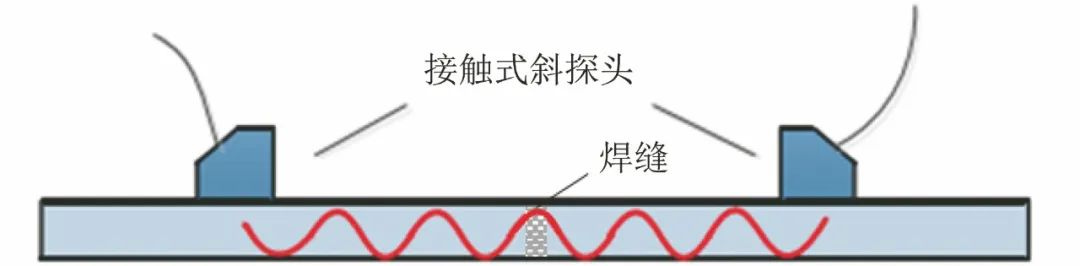
圖3 接觸式雙斜探頭超聲檢測方式示意
03
檢測信號特征分析
信號特征提取算法
采用基于高斯調制脈沖(GMP)模型的信號提取算法對超聲檢測信號進行處理,檢測信號中各回波信號sn(t)可認為具有如下形式:
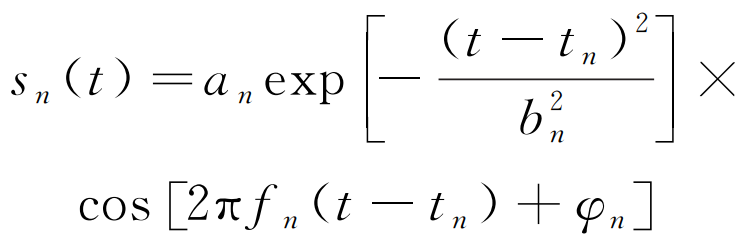
(8)
式中:an為信號幅值;tn為信號傳播時間;fn為信號頻率;φn為信號相位;bn為帶寬因子,與信號的時域波形寬度和頻域帶寬相關。
采用基于GMP模型的信號提取算法,可將各回波信號表示為控制參數(an,bn,tn,fn,φn)的GMP模型,結合互相關濾波估計各控制參數,實現信號特征提取。文章按照如下流程分析檢測信號,并估計信號的非線性特征。
(1) 對于5 MHz的基波信號和10 MHz的二次諧波信號,分別按對應的控制參數生成GMP模型作為參考信號(a0,b0,t0,f0,φ0),其中b0根據信號特點估計得到,即:
① (a0,b0,t0,f0,φ0)5M=(1,0.4,0,5,0);
② (a0,b0,t0,f0,φ0)10M=(1,0.4,0,10,0)。
(2) 計算檢測信號與參考信號的互相關濾波,提取濾波信號最大值出現的時刻作為tn的估計值,根據tn處回波信號的時域與頻域特征估計an和fn;基波信號取n=1,二次諧波信號取n=2,分別估計以上信號特征。
(3) 校核f1是否在(5±0.5)MHz范圍內,f2是否在(10±1)MHz范圍內,如超過該范圍則認為信號提取有誤,需要復核信號提取流程。
(4) 根據超聲波的衰減規律,僅考慮擴散衰減的情況下,超聲波(球面波)的聲壓幅值與傳播距離成反比,筆者對信號幅值進行近似校正,即:
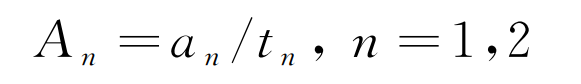
(9)
式中:an以mV為單位;tn以μs為單位進行無量綱處理,計算結果無量綱。
(5) 根據式(7),計算等效非線性系數βe,估計信號的非線性特征,即:
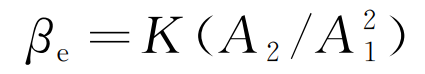
(10)
式中:比例系數K取40。
FSW焊接試件檢測信號特征
以0%壽命階段的某一試件為例,5 MHz和10 MHz檢測信號中的典型回波與選用的參考信號波形如圖4所示。由圖4可看出,參考信號與檢測信號的相似度較高,可獲得較好的濾波效果。
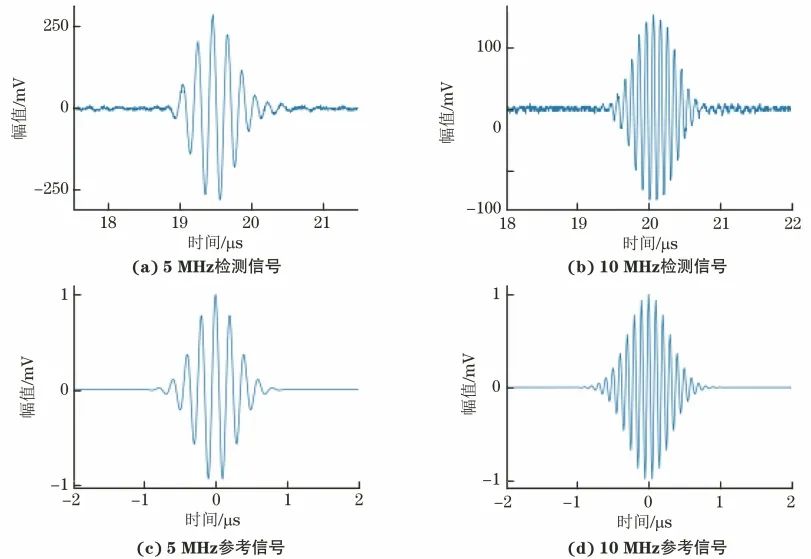
圖4 5 MHz和10 MHz參考信號與檢測信號波形(以0%壽命階段為例)
按照前述算法,根據各階段試件檢測信號計算βe,可得到βe與各疲勞階段的相關關系,如圖5所示。由圖5可以看出,βe隨著疲勞次數的增加而逐漸增大,不同疲勞階段的βe具有一定的區分度。
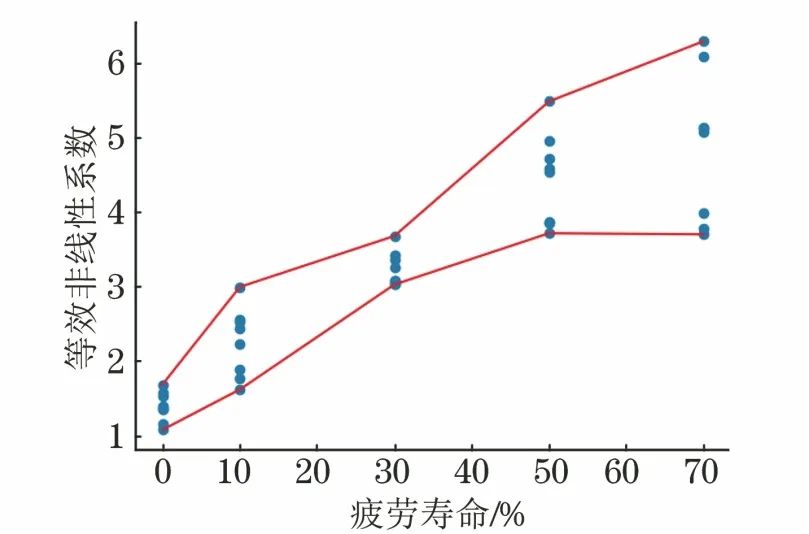
圖5 βe與各疲勞階段的相關關系曲線
04
FSW接頭的疲勞壽命評價方法
貝葉斯定理
根據各疲勞階段的βe數據分布規律,分析可得到任一FSW接頭處于各疲勞階段的可能性,由此即可實現焊縫疲勞壽命的評價。該評價需要估計某一βe=x的焊縫處于疲勞階段i的概率P(i|x)(i=0%壽命,10%壽命,30%壽命,50%壽命,70%壽命),這實際上是一個基于給定指標的分類問題。
根據貝葉斯定理,P(i|x)可稱為后驗概率,有如下關系:
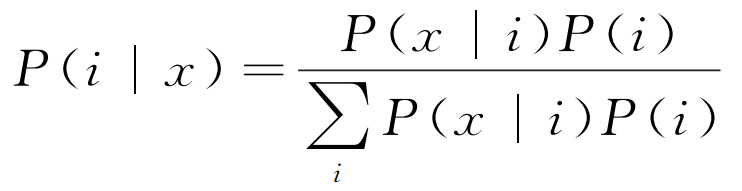
(11)
式中:P(x|i)稱為先驗概率,表示已知焊縫處于疲勞階段i時,該焊縫的βe值等于x的條件概率;P(i)稱為分類概率,表示疲勞階段i出現的概率;可假定各階段的分類概率相等。
由于總體樣本的數據分布情況未知,這里假定各疲勞階段的P(i)相等,因此通過P(x|i)即可求得P(i|x);而估計P(x|i)則需要由各疲勞階段FSW接頭的βe構成基礎數據庫,分析βe的分布規律。
基礎數據庫構建
焊縫疲勞壽命的評價需要基于完備的基礎數據庫,保證每條焊縫都一定處于數據庫中的某一階段。對前述各疲勞階段所代表的疲勞次數范圍做如下擴展性說明,即可形成完備數據庫:
① 0%壽命:疲勞次數≤0.05N0;
② 10%壽命:0.05N0<疲勞次數≤0.2N0;
③ 30%壽命:0.2N0<疲勞次數≤0.4N0;
④ 50%壽命:0.4N0<疲勞次數≤0.6N0;
⑤ 70%壽命:疲勞次數>0.6N0。
一般而言,隨機變量應服從正態分布,但在樣本量較小的情形下,可改用t分布描述隨機變量的分布情況。疲勞階段i的樣本數量為ni,則P(x|i)可表示成自由度為ni-1的t分布概率密度函數,即:
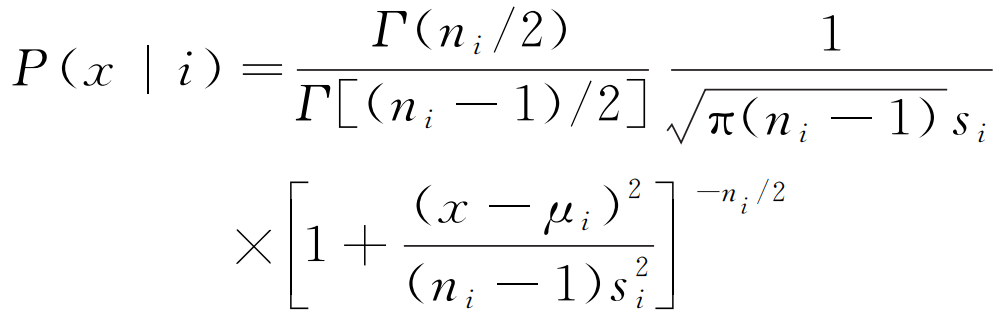
(12)
式中:μi和si分別為βe在疲勞階段i時的平均值和標準差;Γ(z)為Gamma函數。
將疲勞階段i中第j個樣本的βe參數值記為βij,則μi和si可按照以下方式估計:
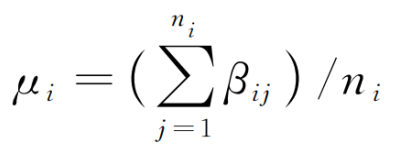
(13)
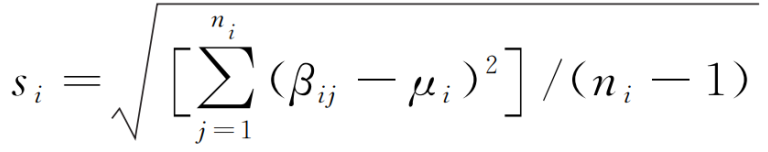
(14)
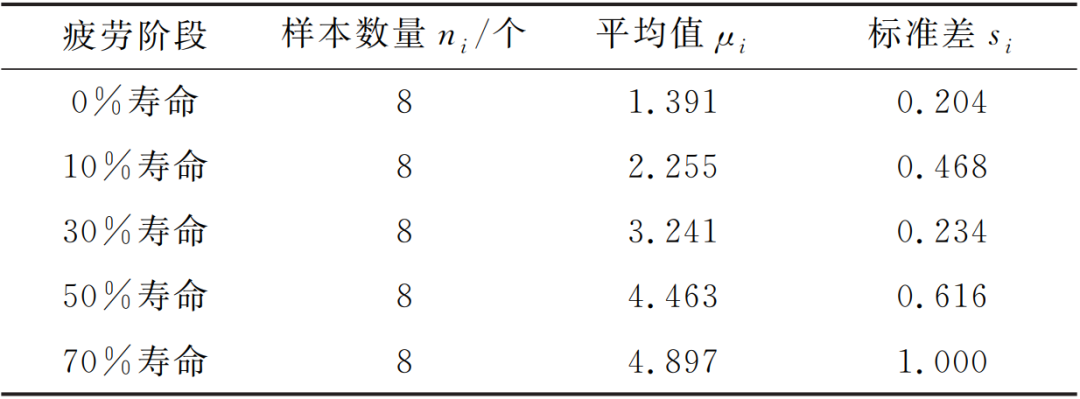
圖5所示的βe值可構成FSW接頭基礎數據庫,其統計信息如表1所示。
表1 FSW接頭基礎數據庫
由式(12)得到βe在各疲勞階段的概率密度分布函數,如圖6所示;進而可根據式(11)計算得到βe在各疲勞階段的后驗概率曲線,如圖7所示。
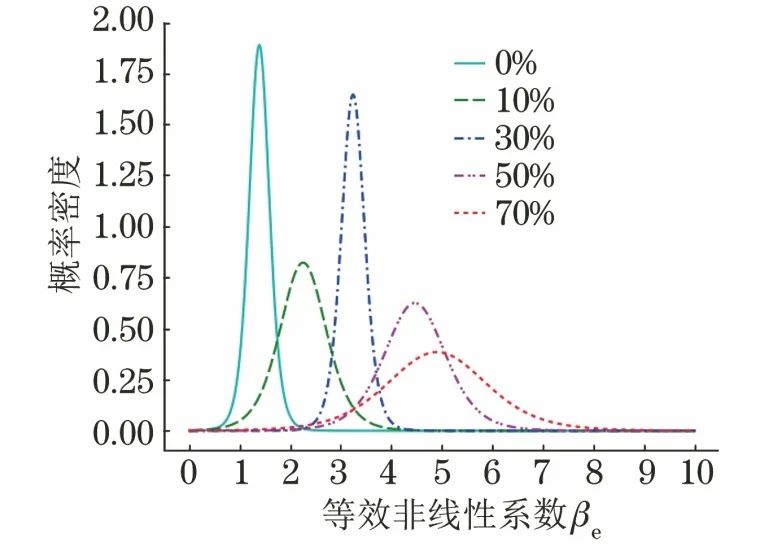
圖6 βe在各疲勞階段的概率密度分布函數
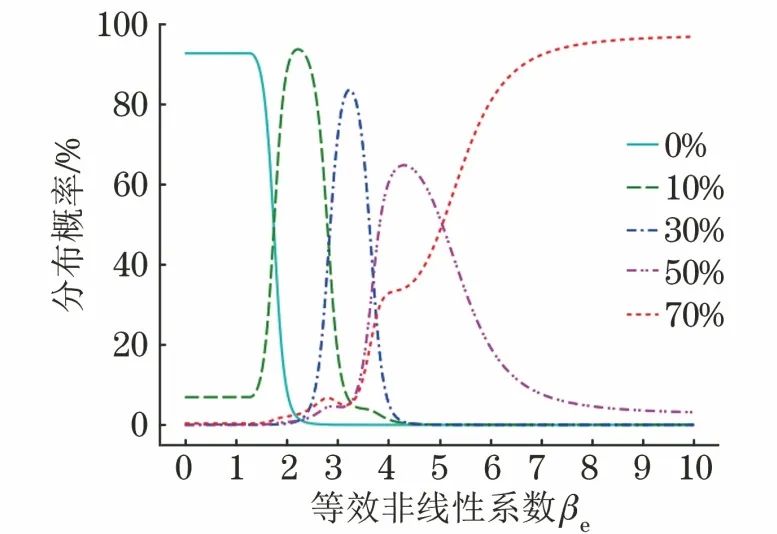
圖7 βe在各疲勞階段的后驗概率曲線(可靠范圍1.0<βe<6.3)
分析上述結果可知:
① βe≤3.5時,焊縫可能以較大概率處于0%壽命,10%壽命或30%壽命中的某一疲勞階段;
② 3.5<βe≤5.5時,由于50%壽命與70%壽命階段的數據重疊較為明顯,焊縫處于這兩個疲勞階段的概率相近;
③ βe>5.5時,焊縫大概率處于70%壽命階段。
需要注意的是,樣本數據范圍是1.0<βe<6.3,超出此范圍的焊縫無法獲得可靠的評價結果,圖7中超出此范圍的概率值僅供參考。
疲勞壽命評價
針對某一類已建立基礎數據庫的FSW接頭,可通過非線性超聲檢測及信號特征分析獲取其βe值,并根據該值估計該焊縫在各疲勞階段的后驗概率,評價焊縫的疲勞壽命。以βe=1,2,3,4,5,6的各條焊縫為例,筆者由圖7中的后驗概率曲線得到相應各焊縫的疲勞壽命評價結果,如圖8所示。
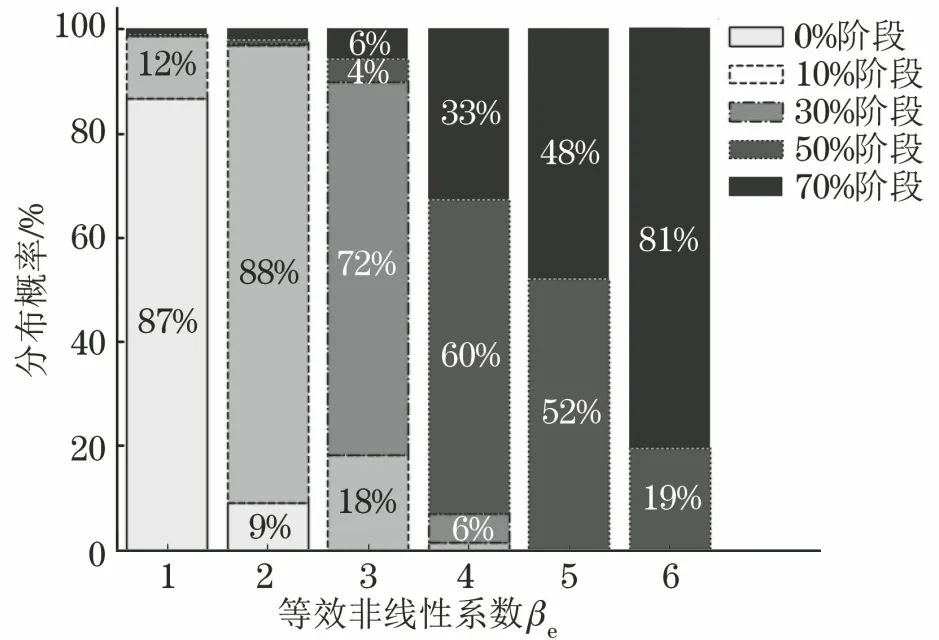
圖8 FSW接頭不同βe焊縫的疲勞壽命評價結果
04
結論
提出了一種基于非線性超聲檢測的FSW接頭疲勞壽命評價方法,該方法采用接觸式雙斜探頭對FSW接頭進行非線性超聲檢測,通過分析信號特征獲取等效非線性系數βe,構建包含多個疲勞階段的基礎數據庫,基于貝葉斯定理估計焊縫處于各階段的后驗概率,評價焊縫的疲勞壽命,主要結論如下:
1
不同疲勞階段FSW焊接試件的非線性超聲檢測信號特征表明,βe參數隨著疲勞次數的增加逐漸增大,該參數對各疲勞階段具有一定的區分度,可用于疲勞壽命評價。
2
βe在各疲勞階段的數據分布規律表明,在數據有效范圍(1.0<βe<6.3)內的大部分區間上,βe對各階段的區分度較好,根據βe可判斷焊縫大概率處于哪一個疲勞階段;其中3.5<βe≤5.5時,由于50%壽命與70%壽命階段的數據重疊較為明顯,焊縫處于兩種階段的概率相近。
3
提出的評價方法可估計焊縫處于各疲勞階段的可能性,最終給出焊縫處于各階段的后驗概率作為評價結果,可作為焊縫分類的參考;但是焊縫分類的具體策略還需要結合大量補充試驗進行設計和驗證。